工厂生产计划的问题说明、数学模型、问题求解
问题说明
在生产规划问题中,需要根据设备、机器维修、材料、工艺流程、销售安排等因素对生产的产品种类、数量、生产能力进行决策和分配,从而实现给定资源下的最大利润。为帮助制造企业更好地决策以上问题,以下述生产场景为例,千江智能给出在工厂生产计划问题的场景化解决方案和求解展示。
假设工厂生产7种产品(产品1至产品7),共有4台磨机(grinders,以下简称GR)、2台立钻(vertical drills,以下简称VD)、3台卧钻(horizontal drills,以下简称HD)、1台钻机(borer,以下简称BR)和1台刨机(planer,以下简称PL)。每种产品的单位利润(定义为单位销售价格减去原材料成本)以及每个工艺所需的生产机器、单位生产时间(小时)如下。
每种产品的单位利润和每个工艺所需的单位加工时间
| 产品1 | 产品2 | 产品3 | 产品4 | 产品5 | 产品6 | 产品7 | |
| 每单位利润 | 10 | 6 | 8 | 4 | 11 | 9 | 3 |
| 磨光(GR) | 0.5 | 0.7 | __ | __ | 0.3 | 0.2 | 0.5 |
| 垂直钻孔(VD) | 0.1 | 0.2 | __ | 0.3 | __ | 0.6 | __ |
| 水平钻孔(HD) | 0.2 | __ | 0.8 | __ | __ | __ | 0.6 |
| 镗孔(BR) | 0.05 | 0.03 | __ | 0.07 | 0.1 | __ | 0.08 |
| 刨削(PL) | __ | __ | 0.01 | __ | 0.05 | __ | 0.05 |
每月可能会有一些些机器将停机维护。这些机器的维护时间和数量计划表如下:
机器维护计划表
| 月份 | 维护机器及数量 |
| 1月 | 一台磨机GR |
| 2月 | 两台卧钻HD |
| 3月 | 一台钻机BR |
| 4月 | 一台立钻VD |
| 5月 | 一台磨机GR和一台立钻VD |
| 6月 | 一台刨机PL和一台卧钻HD |
受到市场需求限制,每种产品每个月最大可销售数量如下表所示:
每种产品每个月最大销售数量
| 产品1 | 产品2 | 产品3 | 产品4 | 产品5 | 产品6 | 产品7 | |
| 一月 | 500 | 1000 | 300 | 300 | 800 | 200 | 100 |
| 二月 | 600 | 500 | 200 | 0 | 400 | 300 | 150 |
| 三月 | 300 | 600 | 0 | 0 | 500 | 400 | 100 |
| 四月 | 200 | 300 | 400 | 500 | 200 | 0 | 100 |
| 五月 | 0 | 100 | 500 | 100 | 1000 | 300 | 0 |
| 六月 | 500 | 500 | 100 | 300 | 1100 | 500 | 60 |
库存容量限制: 每个月每种产品最多100个单位存储量。计划期初没有库存,希望在6月底每种产品都有50个单位的库存量。并且如果产品存放到仓库,每种产品每个月的单位库存持有成本为0.5元。
工作日历: 工厂每周工作六天,可以假设每个月只有24个工作日,每个工作日两班8小时。
为了使总利润最大化,工厂应该何时生产多少数量的何种产品?
单周期问题
产品的最佳组合是一个带有普遍性的优化问题,本次不考虑库存,根据生产能力和市场限制找到最佳方案
数学模型
决策变量: 每种产品的生产量
约束条件:
1、生产能力的约束
根据设备维护和工作日历的限制,工厂的生产能力每个月都不同。
2、市场容量的约束
每种产品的生产量不能超过市场容量的限制
3、非负约束
每种产品的生产量不能为负
目标函数:
我们的求解目标是最大化总利润,即每个月的单位产品销售利润*生产数量最大化。
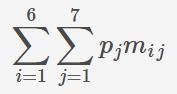 其中pij为每种产品的单位利润,mij为每种产品的生产量
其中pij为每种产品的单位利润,mij为每种产品的生产量
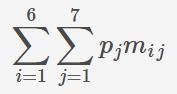 其中pij为每种产品的单位利润,mij为每种产品的生产量
其中pij为每种产品的单位利润,mij为每种产品的生产量
问题求解
对该问题建立数学模型并进行求解,结果如下,总利润期望值24528元。
求解结果:每种产品的生产量
| 产品1 | 产品2 | 产品3 | 产品4 | 产品5 | 产品6 | 产品7 |
| 500 | 888 | 300 | 300 | 800 | 200 | 0 |